Volume 17, June 2023
Learning Strategies for Complex Rhythms: Approaching Richard Barrett's splinter for contrabass solo (2018-2022)

by Kathryn Schulmeister

7. Examples of rhythmic translation in Barrett's splinter

Throughout splinter, many of the measures contain a relatively large number of beats within an odd meter and are challenging to intellectually track in performance given the additional and more pressing task of interpreting the immense amount of rhythmic information written within the lengthy individual measures. For example, in the very first measure of splinter, the meter of the bar is 18/8 (see figure 7), which on its own isn't necessarily a difficult meter for a performer to intellectualize, however given that Barrett intends to create flexible subdivisional grids for rhythm in his work, it naturally follows that after the first note of the piece (which begins on the first beat of the measure, or the "downbeat"), none of the subsequent notes in the measure are articulated on a subsequent eighth note beat of the measure. 

Figure 7: Barrett: splinter,measure 1

In theory, the rhythm problems that present themselves in measures such as the first measure could be manageably addressed with traditional learning methods of breaking down the measure into chunks and learning the polyrhythmic relationships in isolation. This process could then be followed by a process of embodying the rhythmic material and committing the material to memory, slowly assembling the rhythmic material of the measure together in a string of memorized events practiced in isolation. The reality of the learning process, however, proved to be more challenging than a theoretical one. In my initial practice sessions and meetings with my advisor, I rehearsed with a custom made click track that featured 18 beats for the first measure, and I would frequently get lost in the middle of the measure and end up adding or subtracting a beat at some point in the measure. It was clear from the beginning of the learning process that I needed to find a solution to help me train my ability to track the rhythm accurately throughout the measure of 18 beats.  

Tracking the 18/8 meter of the first measure became a performance challenge for me by the second eighth note of the bar, where most of succeeding notes are articulated not only in misalignment with the recurring pulse of the measure (the eighth note), but also with varying polyrhythmic relationships dictated by odd and irregular subdivisions of the common beat. By the end of the second beat of the first measure, the rhythm notated indicates a bracketed 7:6 relationship for the underlying rhythmic figure, meaning that the speed of the 32nd notes within that bracketed figure should be articulated within the timeframe of what would be equal to six 32nd notes at the governing tempo of the measure (in this case, an eighth note = 72bpm). Thus, the tempo of the bracketed figure has a relationship of 7:6 to the governing tempo of the measure. To understand and clearly execute the notated rhythm of this polyrhythmic relationship, the performer must not only keep track of the governing pulse of the measure and how each note relates to that pulse, but also intellectualize and physically mark the rhythmic tempi of the 7:6 relationship as it begins and ends on subdivisions of beats within the measure.

To begin the process of breaking down the material into smaller, more familiar, and thus more comprehensible information, I first made annotations to the score by dividing individual measures into smaller sub-measures. Therefore, I had to choose points to divide the measure into shorter sub-measures where I felt I could accurately relate to and align with as precisely as possible to new downbeats. This process took some trial and error, and at times, I would edit the decisions that I made if I found after a process of experimentation that the re-organization of the measure didn't work well. For the first measure of splinter, I decided to divide the measure into three shorter sub-measures. I translated 18/8 (original meter) into 7/8 + 5/8 + 6/8 (see figure 8). I also calculated how the polyrhythmic material in the measure would relate to the eighth note pulse of the measure and marked in my score an approximate visualization of where the eighth notes I would hear in the click track would align with my performance of the rhythm articulated on the page. Thankfully, Barrett takes great care and works with an extraordinary attention to detail in how accurately spaced his notation of rhythms appears on the page, so I found my annotations of writing in lines to mark the pulsed beats of the bar in line with the notational spacing of the score.

Figure 8: Barrett: splinter,measure 1, with annotations

Translating the meter of 18/8 into three shorter sub-measures allowed me to conceptualize the measure into more comprehensible chunks that I could track with more consistency and accuracy than I could with the original bar of 18/8. I made decisions about how to divide the bar based on several factors. Most importantly, I attempted to annotate and draw new bar lines where I believed I could most accurately align the rhythm written on the score with both my execution and the reference that I would use to monitor the accuracy (whether that was counting in my mind or using the external reference of a metronome/click track). By narrowing my focus on how I counted the rhythm within each bar, I immediately noticed that I was able to train my mind and body to be able to perform the notated rhythms with much more accuracy and consistently.

Although it may seem that translating the 18/8 meter into three shorter sub-measures could potentially alter the phrasing of the measure (it is clear from the score that Barrett intends to a create a gradual consistent build of dynamic intensity and timbral evolution from the precise start to finish of the measure), I argue that it's possible to take into consideration how the phrases are constructed, and to phrase across the annotated bar lines to make the intended shape of the composition. In the same way that one could connect the material of multiple measures under a phrasing line, a performer can make the full phrase of the 18/8 bar come to life while using the translated meters method to aid rhythmic accuracy.

This method of meter translation combined with the use of a custom made click track that I built for practicing and learning this piece (which I will discuss in much more detail in a subsequent section) allowed me to practice aligning certain rhythmic landmarks in the measure to gauge my accuracy and understanding of the rhythm as I practiced. Since I quickly found this method of meter translation to be effective, I continued to apply this process to the rest of splinter as was necessary, which given the hyper complexity of the piece proved to be necessary in nearly every measure of the work.

In the second measure of splinter, I applied nearly the exact same strategy that I applied in the first measure in that I broke down the long measure into three shorter sub-measures, however since the second bar has not only an odd meter but also a different subdivision of the pulse marked by the meter of the bar, my approach slightly altered to fit the exact rhythmic challenges of the second measure. In measure 2, the meter of the bar is 23/16 (see figure 9), however the tempo (indicated as a tempo change in the score) is expressed in eighth notes as an eighth is equal to 81bpm. Given that the tempo is both faster than the initial tempo of the piece and expressed in eighth notes, I decided to once again build the click track in eighth notes for the majority of the second measure, save for the very last three sixteenth notes of the bar, which need to be articulated as both smaller subdivisions and in an odd number to accommodate for the odd meter of the bar in sixteenth subdivisions.

Figure 9: Barrett: splinter, measure 2

Unlike in measure 1, I was able to determine two strategic internal points of measure 2 to align with downbeats of smaller sub-measures. From the original metric structure of 23/16, I translated measure 2 into three shorter sub-measures: 5/8 + 5/8+ 3/16 (see figure 10). In this case, the articulated beat of the third measure within the original measure 2 is measured in 16th notes, which works well in preparing the tempo for the following four measures, which all have unique lengths expressed with 16th note subdivisions of the same general governing tempo of an eighth note equals 81bpm.

Figure 10: Barrett: splinter, measure 2, with annotations

In the third measure of splinter, I continued to apply my method of breaking down measures into shorter sub-measures, and I also applied a new process of translating polyrhythmic material into distinct tempo values for part of the measure. Within measure 3 (see figure 11), there is a bracketed rhythm which indicates that the durational value of the nine notated 32nd notes within that bracket should occur within the exact time frame of seven 32nds at the governing tempo of the bar (in this case, eighth note = 81bpm, or sixteenth note = 162bpm).

Figure 11: Barrett: splinter, measure 3

Considering that not only would the 9:7 ratio be extremely challenging for me to intellectualize and technically perform, but also that within that bracket there is also another indicated polyrhythmic ratio of 5:4 (expressed in sixteenth notes), I decided to translate the 9:7 ratio to a new localized tempo of 208.3 bpm for the bracketed material. I calculated the new tempo by solving for the tempo variable of the bracketed 16th note as it relates in a 9:7 ratio to the original 16th note tempo of 162 bpm (calculated from the tempo marking of an eighth note is equal to 81 bpm). The equation to solve for the tempo (x) of the new 16th note within the bracketed material in measure 3 works as follows:

With the tempo of the 16ths within the bracketed material calculated, I could then learn the rhythmic material within the bracket as it relates to the new tempo of 208.3, rather than as a ratio of 9:7 to the original tempo of the measure. I combined this method of rhythmic translation, in this case rhythmic ratio to tempo, with the meter translation method. I divided measure 3 into three shorter sub-measures, 2/16 + 9/16(with the new tempo of 208.3) + 2/16 (see figure 12). To clarify, the two 2/16 measures that frame the 9/16 measure are both in the original tempo of the section, with the sixteenth note equal to 162 bpm. The reason that I decided to create two 2/16 bars instead of two 1/8 bars is because I needed to understand the sixteenth subdivision of the eighth note to perform the written material of the measure (i.e., I didn't have the temporal context to be able to perform those rhythms accurately without subdivision). In theory, I could memorize the eighth note tempo and perform a subdivision of that tempo but given that tempi for this piece change rapidly and nearly every measure, I felt it was more time efficient and technically accurate to train myself to think in sixteenth notes for this measure.

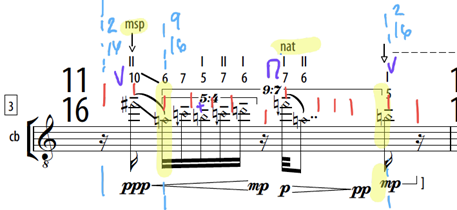Figure 12: Barrett: splinter, measure 3, with annotations

I applied the exact same method of rhythmic translation in measure 9 as I did in measure 3. Measure 9 (see figure 13), a measure of 21/16, features three separate brackets with varying rhythmic ratios.

Figure 13: Barrett: splinter,measure 9

Since the first ratio of 3:2 in terms of eighths notes is a standard polyrhythm that most musicians trained in Western music can perform by memory, I decided not to calculate the new tempi for the bracketed material at the beginning of the measure and instead grouped together the first three eighth note beats of the bar as the first sub-measure of measure 9. I then calculated the tempi of the new sixteenth notes within the following bracketed material with the ratios 9:7 and 10:7 and created sub-measures of 7/16 and 5/8 for the rest of measure 9, with the sub-measures beginning at the start of each of the bracketed sections. I decided to make the third sub-measure of measure 9 a 5/8 bar instead of a 10/16 bar because the tempo of the new sixteenth note was 257.2 bpm and I found it be more effective to subdivide the new eighth note pulse of 128.6 bpm as a reference tempo instead.²⁴ Therefore, measure 9 (see figure 14) became a measure of 3/8 + 7/16(new tempo of 157.5) + 5/8 (new tempo of 128.6).

Figure 14: Barrett: splinter,measure 9 with annotations

The methods I've explained and exemplified with my analyses of measures 1, 2, 3, and 9, apply to most of the rhythmic challenges in splinter save for the cases in which I needed to apply the third method of rhythmic translation: translating the durations of groups of notes into rhythmic subdivisions of tempi. This third method first became necessary in strategizing an approach to learn the rhythmic material in measure 13, and subsequently became useful for more occasions in the subsequent parts of splinter. Measure 13 (see figure 15) presents an unprecedented rhythmic challenge within splinter in that it features a string of rapid notes (entirely made of variations of sixteenth and thirty-second notes) in groups of either odd numbers or within brackets notating polyrhythmic ratios to odd numbers of beats or subdivided beats within the bar. This presents a situation where neither a meter translation nor a translation of polyrhythmic ratio to tempo solves the problem of creating a comprehensible translation of the rhythmic material for the understanding and performance of the measure.

Figure 15: Barrett: splinter,measure 13

To solve this problem, I decided to use a process of translating the duration of groups of note values into tempi, in order for me to then be able to understand the note values as subdivisions of the calculated tempi, rather than in relation to the governing tempo of the bar. For the groups of notes that were direct subdivisions of the governing tempo (an eighth note equal to 81bpm), I grouped the notes together based on their notational barring (connection by notational stem) and calculated the total duration of the grouped notes. For example, the first three thirty-second notes of measure 13, each with an individual durational value of 324 bpm, could be instead interpreted as three equal subdivisions of a single beat of 108 in value (equal to a dotted sixteenth note). With this same process, I calculated the durational value of each group of notes within the measure, which solved the rhythmic problems of the bracketed polyrhythmic note groupings within the bar. For the note groupings written within the brackets of 4:3, 4:5, and 5:4, I calculated the durational value of each bracketed group, which then allowed me to interpret the rhythm as equal subdivisions of the calculated duration. For example, in the portion of the measure where there are four thirty-second notes written under a bracket that indicates the polyrhythmic ratio of 4:3, I calculated that the duration of the group of four notes needed to occur within the same duration as three thirty-second notes at the governing tempo of the bar (which also happens to be the same duration as the first note grouping of the measure), therefore, those four notes could be interpreted as four equal subdivisions of the pulse 108 bpm. I applied the same process of translating the duration of groups of note values into tempi for the entire measure and added an additional pulse for the duration of the sixteenth rest at the end of the measure (see figure 16). Measure 13, originally a 19/16 measure, became a measure of 10 beats of varying durations defined by rates of bpm: 108 + 81 + 64.8 + 108 + 81 + 64.8 + 108 + 81 + 64.8 + 162.

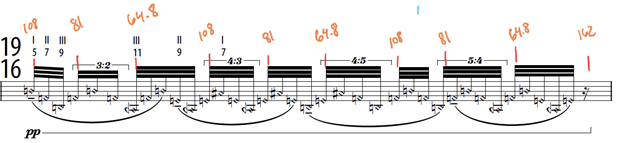Figure 16: Barrett: splinter,measure 13 with annotations

In practice, I trained myself to memorize the tempi to perform the various subdivisions of unprecedented, individualized pulses. The most important feature of this solution, however, proved to be just the ability to intellectually understand how to approach the rhythms with confidence and measurable accuracy.

With the tools of multiple methods of rhythmic translation that I developed in the first part of splinter, I successfully integrated all three methods into measures that presented multifaceted rhythmic challenges and complexities. Measure 23 (see figure 17) is an example of some of the most complex rhythmic puzzles that need to be deciphered in splinter.

Figure 17: Barrett: splinter,measure 23

The primary challenge with measure 23 is that beyond the complexities of the playing techniques involved (multiple stops, microtones, artificial harmonics, etc.), there are multiple layers of polyrhythmic ratios nested within each other within an already challenging meter of 23/16. My strategy in deciphering the rhythmic material within measure 23 was to first address the nested polyrhythms of 8:10 and 6:4 within the bracketed polyrhythm of 8:7. Within this one bracket of material, I combined all three methods of rhythmic translation: First, I translated the 8:7 into three sub-measures of 5/32 + 6/4 + 3/23. Second, I calculated the durational value of the 8:10 grouping of notes (82.28bpm) and the value of the three thirty-second notes into a tempo value (137.13bpm) for a single beat that could then be subdivided by the notes within the groupings (82.28bpm), and third, I calculated the tempi for 6:4 material such that the eighth note pulse (154.3bpm) for the 3/8 sub-measure covering that grouping would reflect the accurate tempo given the multi-layered polyrhythmic information within the score. After organizing a strategy for this bracket of material, I then addressed the rest of the measure, which still featured numerous other complexities and challenges. Over the course of the entire measure, I translated the 23/16 meter into nine sub-measures (see figure 18) with the meters of 3/8 + 3/16 (click for whole bar equals 80bpm) + 1/16 (new tempo of 240) + 1/16 (new tempo of 180) + 1/8 (new tempo of 90) + 5/32 (click for whole bar equals 82.28bpm) + 3/8 (new tempo of 154.3) + 3/32 (click for whole bar equals 137.13bpm) + 5/16 (new tempo of 150).

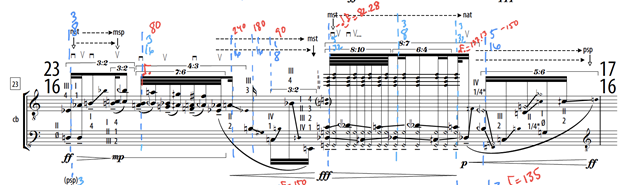Figure 18: Barrett: splinter,measure 23 with annotations

For the first bracketed material of the measure, I calculated the tempo of an eighth note in the 3:2 bracket as 135bpm, which helps with the subdivisions of the individual eighths within the bracket. In the second bracketed material of the bar, a 7:6 bracket is nested within the 4:3 bracket. In this case, I divided the 4:3 bracket into two sub-measures and solved the challenge of the nested 7:6 bracket by calculating the duration of the entire group of seven thirty-second notes, which came out to be equal to the durational value of 1 beat at 80 bpm. With this solution, I annotated the score by translating the 7:6 into a bar of 3/16 and decided to only reference the entire duration of the bar with one beat of 80bpm. Therefore, I could understand and practice interpreting the rhythm as seven equal subdivisions of a single beat of 80bpm. Given that the final sixteenth note within the 4:3 bracket is not a part of the 7:6 bracket, and it does not share a durational value nor a comprehensible relationship to the preceding rhythmic material, I decided to give that note a dedicated individual sub-measure and pulse (a sixteenth equal to 240bpm) calculated to reflect the 4:3 relationship to the tempo of the measure. I also decided to give the subsequent sixteenth note similar treatment and annotated the measure to include a second 1/16 measure, with a pulse reflecting a sixteenth note at the governing tempo of the measure, 180bpm. For the following 3:2 bracket, I decided to make the bracketed material fit within a sub-measure of 1/8 at the tempo of the measure, 90bpm. For the final bracketed segment of measure 23 I translated the 5:6 ratio to a new tempo of 150 for the sixteenth note within the bracketed material and annotated the score to make the last note grouping of the bar a sub-measure of 5/16.

I applied these three strategies of rhythmic translation (meter translation, polyrhythmic ratio translation, and durational grouping translation) to the entire score of Barrett's splinter and made decisions about which methods to use based on the specific challenges of each measure. In the sections that follow, I will describe how I built the click tracks for learning splinter, my practice strategies, and my conclusions about the learning process.